Równanie Clapeyrona

„- Pewnie nie znacie tej bajeczki?

- Znamy.

- Słuchajcie więc…”

Aleksander Fredro „Pan Jowialski”

I tak, cytując Mistrza, mógłbym i Was zapytać, czy znacie tytułowe równanie, choć z pewnością już się z nim zetknęliście, albo nieuchronnie wkrótce je poznacie. Jest ono bowiem tak niezmiennym elementem szkolnej nauki chemii, jak twórczość hrabiego Fredry na języku polskim (choć wydaje mi się, że akurat raczej dotyczy to „Zemsty” niż „Pana Jowialskiego”).

Równanie to można przedstawić na kilka sposobów, na przykład tak:

pV/nT = const.

albo pV=nT*const.

I teraz właściwie wystarczy tylko objaśnić czym są użyte w tytule p, V, n, oraz T i po sprawie, czyż nie? No właśnie nie, bo poznać równanie, a je zrozumieć, to często dwie różne sprawy…

To zacznijmy może od wyjaśnienia kontekstu tego tajemniczego wzoru. Otóż jest ją najprostszą formą, w jakiej można zapisać zależności pomiędzy trzema podstawowymi parametrami opisującymi gaz: ciśnienie (p), objętość jaką zajmuje (V), ilość cząsteczek jaka go tworzy (n) oraz jego temperaturę (T). Samo słówko const. to skrót od łacińskiego słowa „constans”, czyli „stały” i używa się go w naukach ścisłych by zaznaczyć, że dana wielkość jest niezmienna, czyli właśnie stała.

Wiedząc już, co oznaczają poszczególne symbole w równaniu, możemy przystąpić do jego opisu i interpretacji. Moglibyśmy więc powiedzieć, że iloczyn ciśnienia gazu i objętości jaką on zajmuje jest proporcjonalny do iloczynu ilości cząsteczek gazu i jego temperatury. Inaczej mówiąc kiedy dwukrotnie wzrasta pierwszy z iloczynów, czyli ten ciśnienia i objętości) to również dwukrotnie musi wzrosnąć iloczyn liczby cząsteczek i temperatury.

Zastanówmy się teraz, jakie wnioski można wyciągnąć z tego równania. Dla wygody i przejrzystości będziemy przyjmować, że tylko dwie wielkości obecne w równaniu ulegają zmianie, a dwie pozostałe pozostają stałe. Ponieważ zwykle rozważamy pewną konkretną „porcję” gazu to jedną z tych stałych wartości jest zwykle n – liczba cząsteczek. Wyjątkiem od tej reguły jest sytuacja, kiedy liczba cząsteczek ulega zmianie, np. w wyniku reakcji chemicznej.

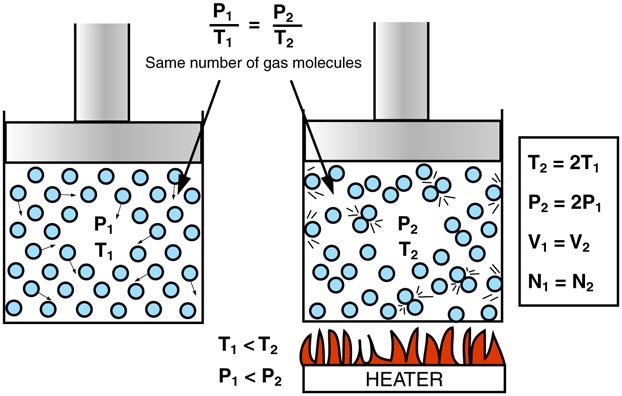
No dobrze, to zacznijmy może od przypadku, kiedy pewną ilość gazu zamkniętej w pojemniku o sztywnych, nieulegających odkształceniu ściankach (czyli o stałej objętości V) będziemy podgrzewać (będzie rosła temperatura T). Rzut oka na równanie Clapeyrona i już widzimy, że musi wzrosnąć p, czyli ciśnienie.  To dlatego wszelkie szczelnie zamknięte pojemniki (szczególnie te zawierające gaz pod ciśnieniem) należy trzymać z dala od źródeł ciepła, a zwłaszcza ognia, ponieważ grozi to eksplozją pojemnika. Dodajmy jeszcze, że zasada mówiąca, że wzrost ciśnienia gazu, przy jego stałej objętości, jest proporcjonalny do wzrostu temperatury nazywamy prawem Charles’a (od nazwiska odkrywcy – francuskiego fizyka Jacques’a Charles’a). Jakkolwiek w źródłach anglojęzycznych jest ono nazywane prawem Gay-Lussaca.

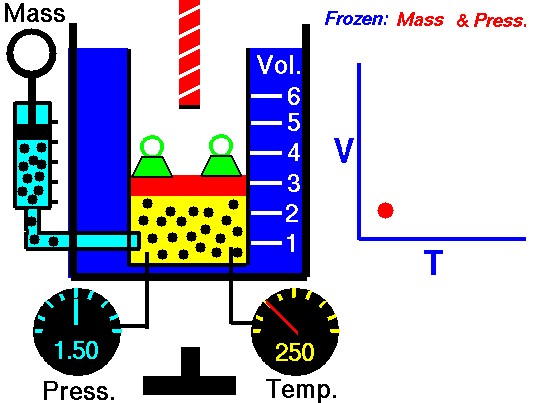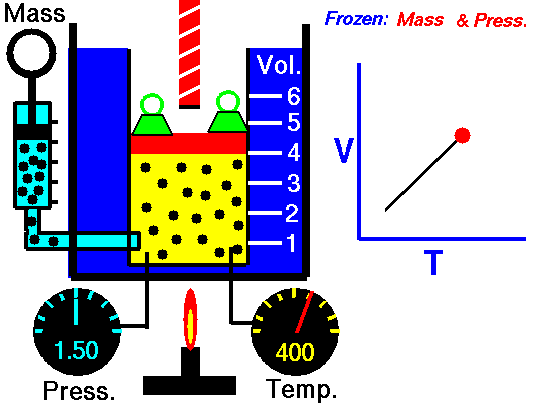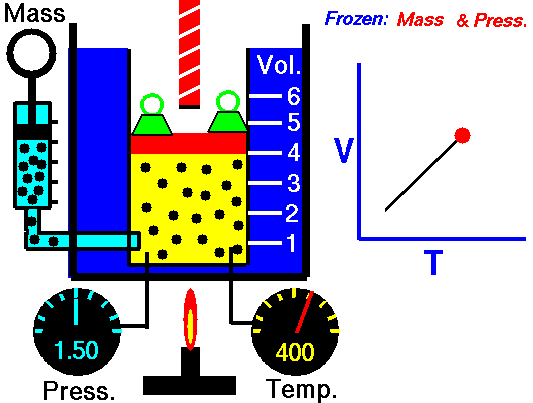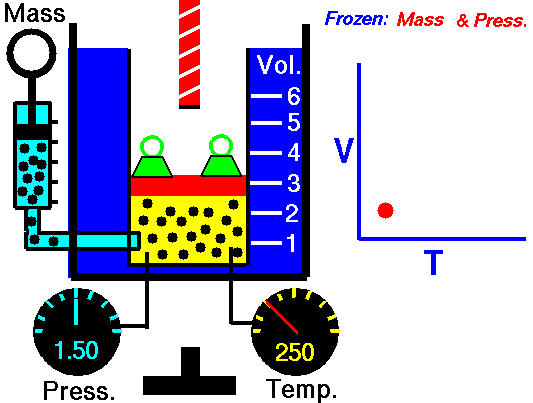
Drugi przypadek jest podobny, to znaczy taki, w którym również zwiększamy temperaturę, ale utrzymujemy stałe ciśnienie. Taki proces nazywamy izobarycznym (od greckich słów isos ἴσος „równy” i baros βάρος „ciężar, ciśnienie”). Co będzie się wtedy działo z objętością? Tak, zgadliście! – będzie rosła. Taka reguła nazywana jest prawem Gay-Lussaca (albo prawem Gay-Lussaca-Charles’a w świecie anglosaskim). Oczywiście ta zasada działa również w drugą stronę – jeśli oziębimy gaz to przy stałym ciśnieniu jego objętość będzie maleć. Łatwo to zaobserwować, kiedy np. nadmuchany balonik i włożymy go na jakiś czas do zamrażalnika. Gwarantuję, że się skurczy.

Jest jeszcze trzecia opcja, tzw. proces izotermiczny, czyli przy stałej temperaturze. I tu, uwaga, zależność między ciśnieniem a objętością nie jest proporcjonalna, a odwrotnie proporcjonalna. Już tłumaczę o co chodzi.

Rzecz w tym, że iloczyn ciśnienia i objętości musi być stały, a więc jeśli będziemy zmniejszać objętość gazu to ciśnienie gazu musi wzrosnąć (jak w pompce do roweru). I odwrotnie, gdy na przykład będziemy zwiększać objętość gazu to jego ciśnienie będzie maleć. Tą z kolei zależność zwykło się nazywać prawem Boyle’a (w krajach anglosaskich, ponieważ był to Anglik) albo prawem Mariotte’a (we Francji, bo to Francuz) albo prawem Boyle’a-Mariotte’a (np. w Polsce).

W porządku, ale tyle się rozpisałem, a nie wspomniałem istotnej rzeczy, a mianowicie, że cały te wszystkie prawa oraz samo równanie Clapeyrona (skądinąd autorstwa też Francuza, Benoît Clapeyrona), dotyczą gazu doskonałego. Pod tym terminem mamy na myśli gaz o cząsteczkach, które są:

1. nieskończenie małe,
2. nie oddziałują ze sobą poprzez jakiekolwiek siły (z wyjątkiem odpychania w momencie zderzeń),
3. doskonale sprężyste (czyli odbijają się od siebie bez strat swojej energii),
4. w ciągłym ruchu.

Nie muszę chyba mówić, że tak po prawdzie… taki gaz nie istnieje. Choćby dlatego, że cząsteczki gazów rzeczywistych mają jakiś rozmiar (choć niewielki z naszego punktu widzenia). Niemniej gazy rzeczywiste z całkiem dobrym przybliżeniem można traktować jako gazy doskonałe. Takie uproszczenie jest szczególnie uzasadnione kiedy zmiany poszczególnych parametrów, tj. ciśnienia, objętości lub temperatury, są względnie niewielkie. Dodatkowo gazom rzeczywistym bliżej do gazu doskonałego, jeśli ich cząsteczki są małe. To oznacza, że równanie Clapeyrona dokładniej opisuje gazowy wodór czy hel, niż np. butan.

Na koniec trzeba by jeszcze wrócić do owego „const.”, obecnego w równaniu Clapeyrona. Ma ono swoją nazwę (to stała gazowa lub stała Clapeyrona) oraz konkretną wartość i wymiar (w przybliżeniu 8,3 J/(mol*K)). Zwykle też oznacza się tą stałą wielką literą „R”. Wówczas równanie Clapeyrona przybiera swoją najpopularniejszą postać: pV=nRT.

Równanie to, którym tak niemiłosiernie męczy się młodych adeptów fizyki i chemii, może się wydawać dość banalne (szczególnie jak je sobie objaśniliśmy). Ale nie dajcie się zwieść, tkwi w nim potężna siła, bowiem gdziekolwiek mamy do czynienia z gazami tam umiejętność posługiwania się nim jest kluczowa. Czy to będzie zakład dostarczający gaz ziemny do naszych domów, czy produkcja dezodorantów w spreju, czy nawet latanie balonem lub samolotem – prawa gazowe obowiązują wszędzie tak samo. Dotyczy to również turbin parowych w elektrowniach i silników spalinowych w naszych samochodach, a to już, przyznajcie sami, są sprawy naprawdę dla nas ważne…

Wojciech Smułek

6.06.2022 r.